데이터 분석 학습일지🐣

7일차 - 데이터 분석을 위한 기초 수학/통계(1)

boiled egg 2023. 6. 28. 19:02

Date : 2023-06-28

Topic : 기초 통계, t-test, 회귀 분석

Note 

통계학

: 표본을 수집, 분석하여 특성을 파악하고 이를 통해 모집단의 특성에 대해 추론.
  자료에 근거한 합리적인 의사결정을 목적으로 함.

통계는 완벽하지 않다.
  • 통계학의 분류
    • 기술 통계학 : 요약 통계량, 그래프 표 등을 이용해 데이터를 시각적 표현, 정리, 요약하여 데이터 전반적인 특성 파악
    • 추론 통계학 : 추출된 표본을 사용하여 모집단의 특성을 파악하는 방법. 점 추정, 구간 추정을 하거나 가설을 검정

모집단과 표본

  • 모집단 : 아직 가지고 있지 않은 모르는 데이터를 포함한 모든 데이터 = 관심의 대상이 되는 집단!
  • 표본 : 모집단 전체를 분석하기 위한 일부 데이터

확률

: 어떤 일이 일어날 경우의 수, 가능성

표본 공간(일어날 수 있는 모든 경우의 수) - 실험(결과를 예측할 수 없는 어떤 행동을 취하는 것) - 사건(실험에 의해 벌어진 일이나 그 값)

 

  • 확률 변수 : 확률적 법칙에 따라 변화하는 값

호수의 전체 물고기 중 몸길이가 3cm인 1마리를 낚아 올림

                        모집단                                                 실현값             표본                    샘플링

 

우리는 내일 낚시를 할 때 몇 cm의 물고기를 잡을 수 있을지 알 수 없음 = 확률 변수!

 

  • 확률 분포 :확률 변수와 그 값이 나올 수 있는 확률을 대응시켜 표시한 것

복원 샘플링/비복원 샘플링

  • 복원 : 한번 뽑은 표본을 다시 모집단에 포함시켜 다음 표본을 샘플링

  • 비복원 : 뽑은 표본을 제외시키고 샘플링 (첫번째 뽑기와 두번째 뽑기의 확률이 달라짐)

  • 도수 : 데이터가 나타낸 횟수 = 빈도를 숫자로 표현!

히스토그램

  • 기댓값 : 나올 것으로 기대되는 평균 값
  • 중앙값 : 주어진 값들을 크기 순으로 정렬했을 때 가장 중앙에 위치하는 값

  • 대표값으로서의 평균과 중앙값
    : 평균은 모든 데이터를 포함한 개념이지만 특잇값에 취약하고,
    중앙값은 모든 데이터를 포함하진 않지만 특잇값에 강건함.(로버스트)

  • 분산⭐
    데이터가 < '평균(기댓값)'과 얼마나 떨어져 있는가 > 를 나타내는 지표
    → 분산이 클수록, 데이터들이 평균값에서 멀리 떨어져 있음

  • 표준편차 : 분산의 제곱근
    → 분산을 계산할 때 데이터에서 평균을 뺀 값을 제곱하는 이유는 결과값의 부호를 없애기 위함 (절대값은 미분이 불가능해 계산할 수 없으므로 사용 X)
    → 결과적으로 분산은 제곱값이므로 사용하기 불편하여 표준편차로 변환 후 사용

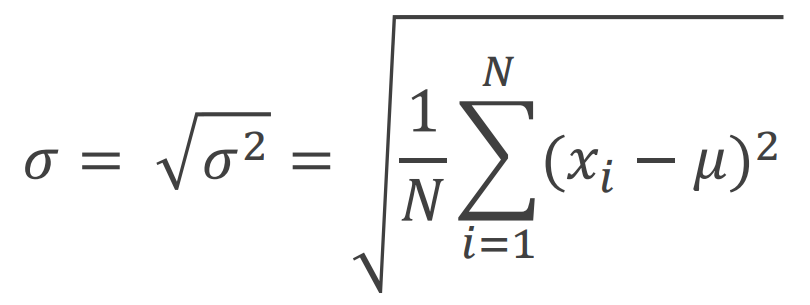
정규 분포

: 연속 확률 분포

  • 정규 분포의 특징
    1. -∞ ~ ∞의 실수 값을 취함
    2. 중앙 부분이 평균이며, 평균을 기준으로 대칭 모양임
    3. 평균값 부근의 확률 밀도가 큼(평균값 주변의 데이터가 많음) → 그래프가 종 모양을 가짐
    4. 표준편차의 값에 따라 정규 분포의 높낮이가 변함 → 표준편차가 높으면 더 퍼진 형태의 종 모양을 가짐
    5. 다양한 정규 분포 중 평균이 0, 표준편차가 1인 분포를 표준정규분포라고 함

이상치

: 정상군의 상하한의 범위를 벗어났거나 패턴에서 벗어난 수치

  • 이상치는 반드시 제거해야 하는가?
    : 분석 결과의 질을 떨어뜨리거나 왜곡시킬 수 있으므로 제거하거나 다른 값으로 대체하는 경우가 많지만,
      상황에 따라서는 제거하지 않고 분석해야 하는 경우도 있을 수 있음.

이상치 제거 여부 예시

👉오로지 데이터 분석가(or 담당자)의 역량

 

  • Z-score : 자료가 평균으로부터 표준편차의 몇 배만큼 떨어져 있는지를 나타내는 지표
  • Z-Score의 특징
    1. 양의 Z-Score는 자료 값이 평균보다 높음을 의미
    2. 음의 Z-Score는 자료 값이 평균보다 낮음을 의미
    3. 0에 가까운 Z-Score는 자료 값이 평균과 비슷함을 의미
    4. Z-Score가 3 이상이거나 -3 이하면 일반적으로 이상치로 판단함
      * 이 기준은 관습적인 지침이므로 절대적인 기준이 아님
      * 상황에 따라 ±2가 기준이 되거나 ±4가 기준이 될 수 있음
  • IQR(Inter Quaritle Range) : 1사분위수와 3사분위수 간의 거리 = 3사분위수(3Q) - 1사분위수(1Q)
  • 사분위수 : 데이터를 4등분한 수치
    • 0.25 / 0.5 / 0.75

Box plot (상자 도표)

: 5개의 수치적 자료를 활용해 데이터의 분포와 범위를 표현한 그래프

상관 계수

: 두 변수 사이 상관성 ( -1 ≤ r ≤ 1 )

1에 가까울 수록 양의 상관 관계(정비례), -1에 가까울수록 음의 상관 관계(반비례)

  • 일반적으로 상관 계수가
    • 0.7 이상 강한 양의 상관 관계
    • -0.7 이하면 강한 음의 상관 관계
  • 상관 분석 : 두 변수 간에 어떤 선형적 또는 비선형적 관계를 갖고 있는지를 분석
  • 상관 관계 : 한쪽이 증가하면 다른 쪽도 증가하거나, 반대로 감소되는 경향을 인정하는 두 양(量) 사이의 통계적 관계
    → 두 변수가 선형 관계에 있는지 비선형 관계에 있는지 파악
  • 상관 계수표 : 분석 대상 변수들의 상관 관계를 한 눈에 보여주는 표 (조건부 서식 - 색조 3가지 - 숫자 -1 ~ 1)

가설 검정

: 통계적 추론의 하나, 표본 정보를 사용해 가설의 합당성 여부를 판정하는 과정

  • 귀무 가설 : 기본적으로 참으로 추정되며 처음부터 버릴 것으로 예상하는 가설(차이가 없거나, 의미 있는 차이가 없는 경우)
  • 대립 가설 : 귀무 가설에 대립하는 명제. 보통 독립 변수와 종속 변수 사이에 어떤 특정한 관련이 있다는 결과가 도출됨. 귀무가설을 기각하는 반증의 과정을 거쳐 참이라고 받아들여질 수 있음

대립 가설  ↔  귀무 가설

         우리가 주장하는 가설  ↔  일반적으로 인정되는 사실

  • 대립 가설의 종류(3가지 형태)
    • ex) 귀무 가설
      : 우리나라 남학생의 신장 평균(μ)은 170cm이라는 가설의 검정 (      𝐻0 : μ = 170)
      • 제 1형 : 𝐻1 : μ ≠ 170 → 양측 검정
      • 제 2형 : 𝐻1 : μ < 170  → 단측 검정
      • 제 3형 : 𝐻1 : μ > 170 → 단측 검정

귀무 가설의 평균이 아닐 것이다 - 양측 검정

귀무 가설의 평균보다 작거나 크면 - 단측 검정

  • 검정의 기준 p-value(유의 확률)⭐
    : 귀무 가설이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 '같거나 더 극단적인' 통계치가 관측될 확률
    • ex) 농장을 구입하기 위해 농장 주인과 대화하던 중, 농장 주인은 자신의 농장에 총 10,000마리의 돼지가 있고 평균 체중은 100kg이라고 말했다.
    • 귀무 가설 : 돼지 10,000마리의 평균 체중은 100kg이다.
      귀무가설이 참인지 증명하기 위해 무작위로 돼지 100마리를 선정해 평균 체중 측정 (100마리씩 여러 번 표본 선정)
      1. 표본에 따라 다양한 평균값이 나올 수 있음
      2. 하지만 전체 평균이 진짜 100kg라면 표본의 평균값도 100kg 근처에서 형성될 가능성이 큼
      3. 전체 평균이 진짜 100kg일 때, 표본의 평균이 30kg가 나올 확률은 5% 미만임
      4. 그런데 우리가 추출한 표본의 평균이 30kg가 나왔다면?
      5. 전체 평균이 100kg이 아닐 것이라고 강하게 의심
      6. 돼지 10,000마리의 평균 체중은 100kg이라는 귀무 가설을 기각함
      7. 이 때 30kg가 나오거나 30kg보다 더 극단적인 평균이 나올 확률이 p-value

  • p-value 사용 시 주의사항 : 관계나 집단들 사이에 차이가 생겨나는 것이 우연한 것인지, 변수에 의한 것인지 여부를 밝히는 것으로, 효과나 변화의 정도, 관계의 강도나 크기 등을 설명하는 것은 아님
    • ex) 불안감과 직업 만족도를 사이의 관계를 검정한 결과 p-value가 0.05 미만일 때
      • 우리가 알 수 있는 것 : 불안감과 직업 만족도 사이의 관계는 우연히 생겨나는 것이 아니라는 충분한 증거를 가지고 있다는 사실
      • 우리가 알 수 없는 것 : 불안감과 직업 만족도의 관계가 정관계(높은 불안감을 가진 사람이 높은 만족도를 가지고 있는지)인지, 역관계(높은 불안감을 가진 사람이 낮은 만족도를 가지고 있는지)인지는 알 수 없음

→ 상관 계수 𝒓이나 결정 계수 𝑟^2 등의 지표를 함께 활용해 분석 결과를 더 정확히 표현할 수 있음

 

  • A/B test : 두 가지 처리 방법, 제품, 절차 중 어느 쪽이 다른 쪽보다 좋다는 것을 입증하기 위한 test
    A - 처리군 : 특정 처리에 노출된 대상 집단
    B - 대조군 : 어떤 처리도 하지 않은 대상 집단

t-test

: 두 개 집단 평균에 통계적으로 유의미한 차이가 있는지를 검사

  • ex) A, B 환자군 사이 유의미한 차이(효과)가 있는지
    • A 환자군 - 처방 X → 간 수치 평균
    • B 환자군 - 약 처방 → 간 수치 평균

적합한 t-test 방법을 선택하기 위한 F 검정 필요 : [ 변수 선택 → F검정 → t-test → 결과 해석 ]
(F-검정은 두 집단의 등분산성을 검정해 각 상황에 맞는 t-test 방법을 선정하기 위해 사용!)

  • F-검정
    • 두 집단의 등분산성(분산이 같은지 여부)을 검정
      • P-value > 0.05 : 두 집단의 분산은 같음
      • P-value < 0.05 : 두 집단은 분산은 다름
    • 두 집단의 평균이 유의미한 차이가 있는지 검정
      • P-value > 0.05 : 두 집단의 평균에 유의미한 차이가 없다
      • P-value < 0.05 : 두 집단은 평균엔 유의미한 차이가 있다

F-검정
t-검정

  • ex) 우리 회사의 신약은 질병 치료에 유의미한 효과가 있을까
    • 집단1은 그대로 두고 집단2에 인위적인 처리를 하거나 자연적으로 영향을 주는 사건이 발생했을 때,
      t-test의 P값이 0.05보다 작으면, 집단2에 시행한 처리나 발생한 사건이 두 집단의 평균 차이에 유의미한 영향을 미쳤다고 해석할 수 있음 (다른 외부 요인들은 동일하게 통제되었다는 가정 하에)

< 실습 >

raw data

회귀 분석

: 두 개 이상 연속형 변수인 종속 변수와 독립 변수 간 관계를 파악하는 분석
  두 변수 간 관계 파악 및 미래 값 예측 목적

  • 회귀 분석의 종류
    • 선형 회귀 분석 : 함수식이 선형 함수식일 때 
      • 단순 선형 회귀 분석 : 독립 변수(x)가 한 개일 때 (y와 x 사이의 1차 방정식 구하기)
        3일차 학습일지 참고
      • 다중 선형 회귀 분석 : 독립 변수(x)가 여러 개일 때
    • 비선형 회귀 분석 : 함수식이 선형 함수식이 아닐 때
  • ⭐단순 선형 회귀 분석의 평가와 해석(복습)
    : 결정계수(r^2) / F값 / Y절편 및 X1 계수 확인
    • 결정계수는 0 ~ 1값을 가지며 1에 가까울수록 회귀 모형이 실제 값을 잘 설명함
      ex) 결정계수가 0.937이면 이 회귀 모형이 실제 데이터의 93.7%를 설명할 수 있다는 뜻!
    • F값이 0.05 미만이면 이 회귀 모형이 유의미하므로 사용 가능
      ex) 1.1E-14 = 1.0729984978606E-14 이므로 0.05보다 작음
    • y=ax+b 에서 Y절편은 b값을, X1값은 a(기울기)를 뜻함
      ex) Y절편이 -4.E+07, X1이 56081이면, 회귀 모형식은 y = 56081x -4.E+07

< 실습 >

data

 


y=6.747x + 26205925
R^2=결정계수

  • 다중 선형 회귀 분석에서 조정된 결정계수로 결과를 확인하는 이유
    • 어떤 독립 변수(x)가 종속 변수(y)에 영향을 주는 변수가 아니더라도 독립 변수(x)의 개수가 많아지면 결정계수는 어느 정도 높아지게 됨(오류)
      → 영향이 없는 변수들이 추가되어 결정계수가 높아진 오류분을 조정 반영한 결정계수 확인

오랜만에 수학적인 개념을 머릿속에 넣었더니 힘들었다.. 고등학교 수학 과목도 확통을 제일 안좋아했는데 잊고 있던 개념들+새로 배운 것들이 합쳐져서 과부하가 왔다 ^_^ 그래도 온라인 강의로 예습복습 좀 하고 들었으니 좀 낫겠지! 싶었는데 왜 똑같은 개념을 다시 듣는데도 처음 듣는 것 마냥 새로운지😿 그래서 강의 후반부로 갈수록 집중력이 짧아져서 계속 머릿속을 환기하느라 놓치는 부분도 점점 많아져서 필기를 포기하고 강의만 들었다. 최대한 본강의에서 집중해서 다 끝내고 선택 학습 시간에 못들은 온라인 강의를 다 듣는게 목표였는데 만만하게 봤다가 큰코 다쳤다.

그래도 온라인 강의로 듣던 통계를 실시간으로 들으니 중간중간 질문도 가능하고 p-value 같은 헷갈렸던 개념도 정확하게 설명해주셔서 이해가 됐다. t-test/f-검정 부분은 원리가 이해가 잘 안돼서 일단 개념 자체를 외웠다🥲 규칙처럼... 하다 보면 이해가 되겠지 다시 공부해야 할 것 같다.

저작자표시 (새창열림)